SETS & Permutation and Combination
Principle of Inclusion and Exclusion
Definition: The
number of elements in a set A is denoted by 
. Hence if set A
contains n elements, we write 
.
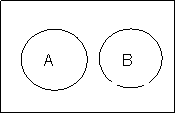
Definition: We say that 2 sets, A and B, are mutually
exclusive if 
.
Hence, given 2 mutually exclusive sets, A and B, we
have 
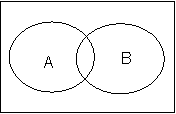
In general, if A and B are finite sets. Then
Let A, B and C be finite sets. Then
Let A, B, C and D be finite sets. Then
Application 1.
Find the number of integers in 
which are divisible by
2,3 or 5.
Let A be the subset of S which contains elements that
are divisible by 2.
Let B be the subset of S which contains elements that
are divisible by 3.
Let C be the subset of S which contains elements that
are divisible by 5.
is the subset of S
which contains elements that are divisible by 6
is the subset of S
which contains elements that are divisible by 15
is the subset of S
which contains elements that are divisible by 10
is the subset of S
which contains elements that are divisible by 30
Hence 
.
Exercise 1
A. Let A,
B and C be finite sets. Prove that
(i) 
;
(ii) 
where A'
and B' are the complements of A and B respectively.
B Apply the result of A(ii) to find the
number of integers from 1 to 250, inclusive, which are not divisible by 2 nor
by 7 but are divisible by 5.
ANSWER 21
Application 2
Let S be the set of 14 students and 
be the properties that a students attends the course
Philosophy, Economic, Chinese respectively.
|
Student |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
4 |
|
|
4 |
|
|
|
4 |
4 |
|
|
4 |
|
|
|
|
4 |
4 |
4 |
4 |
|
4 |
|
4 |
|
4 |
4 |
|
4 |
|
|
|
4 |
|
4 |
|
|
|
|
4 |
4 |
|
4 |
|
|
4 |
Let w(
) denote the number of elements in S satisfying , i =1,2,3
w(
) means the number of elements in S satisfying both , i,j=1,2,3
w(
) = 5 w(
) = 9 w(
) = 6
w(
)=3 w(
)= 3 w(
)= 4
w(
)= 2
The number of students who did not attend any course
=
- { w() + w() + w() }
+ {w() + w() + w() }
- {w()}
= 14 - 20+
10-2 = 2
The number of students who attended exactly one
course =
{ w() + w() + w() }
-
{w() + w() + w()}
+
{w() }
= 20 - 2(10) +3(2) = 6
The number of students who attended exactly two
courses =
{w() + w() + w()}
- 
{w() }
= 10 - 3(2) =4
The number of students who attended exactly three courses=
Exercise 2
Find the number of integers from 1 to 100 inclusive,
which are divisible by
(a)
non of 2, 3, 5?
(b)
exactly one of 2,3, 5?
(c)
exactly two of 2,3,5?
(d)
all of 2,3,5?
ANSWER 26,48,23,3
Let S ={ 1,2,3,….100} and
be the properties that the number is divisible by 2, 3 and 5
respectively.
Application 3
Find the number of arrangement using all letters of
the word MEGAPHONES which contain no pattern of MA, POH and SHEE.
Let S be the set of all arrangement of the given
letters. Let be the properties that the arrangement contains the pattern
MA, POH, SHEE respectively.
Let w() be the number of elements in S satisfying , i=1,2,3. That
is w() means the number of arrangement which contains the pattern
MA.
w() means the number of elements in S satisfying , i,j=1,2,3.
That is w() means the number of arrangement which contains both MA and
POH.
=
= 1 814 400
w()+ w() + w() =
=206 640
w()+w()+w()=
+0= 3240
w()= 0
Hence the number arrangement using all letters of the
word MEGAPHONES which contain no pattern of MA, POH and SHEE =
- { w()+ w() + w() } + {w()+w()+w() } - w()
=161 100
Exercise 3
Find the number of arrangements using all the letters
of the word COMBINATIONS which do not contain any of the pattern BIN, SIN and
TOMB.
ANSWER 56185800
Application 4
Find
the number of integer solutions for the equation 
with 
.
(Remark: The answer to this question is trivial
intuitively since 5+6+7=18 and 
, we can make use of set theory to outline a proof which is
applicable for 
with 
where 
.)
Let
S be the set of all integer solutions for with 
.
Let
be the properties that
respectively.
Let w() be the number of elements in S satisfying .
It can be shown that = 
=
w() + w() + w() =
=
w()+w() + w()=
=
w() = 
=
The number of integer solutions for the equation with is
- { w() + w() + w() } + { w()+w() + w()} - w() = - { } +{ } - = 0
Exercise 4
Find the number of integer solutions for the equation
with 
.
ANSWER 106
Prepared By Ms Khong Beng Choo
Adapted from MQ3207 Combinatorial Analysis,2001