 RAFFLES INSTITUTION
RAFFLES INSTITUTION
GIFTED
EDUCATION PROGRAMME
ADDITIONAL
MATHEMATICS
ASSIGNMENT 3
1. 18 persons are employed by a
company. 11 of them can do shorthand typing and 12 of them can use the word
processor.
(a) If every person has at least one of
these skills, how many persons have all the skills?
(b)
If ![]() persons have none of
the skills, find the greatest possible value of
persons have none of
the skills, find the greatest possible value of ![]() .
.
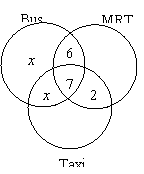 2. A number of travellers were
interviewed about the transport they used on a particular day. Each of them used once or more of the modes of transport shown in
the Venn diagram. Of those interviewed, 6 said that they travelled by
bus and MRT only, 2 by MRT and taxi only and 7 by bus, MRT and taxi only.
2. A number of travellers were
interviewed about the transport they used on a particular day. Each of them used once or more of the modes of transport shown in
the Venn diagram. Of those interviewed, 6 said that they travelled by
bus and MRT only, 2 by MRT and taxi only and 7 by bus, MRT and taxi only.
(a)
Given
that 35 people used buses and 25 people used MRT, find
(i)
the
value of ![]() ,
,
(ii)
the
number of people who travelled by MRT only,
(iii)
the
number of people who travelled by at least two modes of transport.
(b)
Given
also that 85 people were interviewed altogether, calculate the number of people
who travelled by taxi only.
3. In a community club, a group of 40
women takes part in at least one of the three activities: Cooking, Singing and
Dancing. Of the 25 women who choose Cooking, 8 also choose Singing and Dancing,
3 choose Cooking only, 6 choose Dancing but not Singing.
Of
the 15 women who do not choose Cooking, ![]() choose both Singing
and Dancing,
choose both Singing
and Dancing, ![]() choose only Dancing, 5
choose only Singing.
choose only Dancing, 5
choose only Singing.
(a)
Draw
a Venn diagram to illustrate this information.
(b)
Find
the value of ![]() .
.
(c)
How
many women choose Cooking and Singing but not Dancing?
4. In a school, some of the subjects
that are possible to take are Mathematics, Additional Mathematics and Physics.
The Venn diagram shows the combinations of these subjects that are possible and
the numbers and letters represent the numbers of students in each subset.
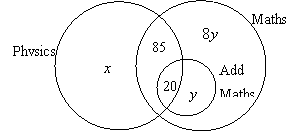
(a)
Given
that the number of students taking Physics is 123, calculate the value of ![]() .
.
(b)
Given
that one-sixth of those taking Mathematics also take Additional Mathematics,
calculate the value of ![]() and hence find the total number of students taking
Mathematics.
and hence find the total number of students taking
Mathematics.
5. By drawing a Venn diagram, or otherwise,
answer the following questions:
(a)
Given
that ![]() ,
, ![]() and
and ![]() , find the least possible value of
, find the least possible value of ![]() .
.
(b)
In a
group of 60 people, 33 can speak Spanish and 36 can speak French. Find the
greatest possible number of people who can speak Spanish, but not French.