 RAFFLES INSTITUTION
RAFFLES INSTITUTION
GIFTED
EDUCATION PROGRAMME
ADDITIONAL
MATHEMATICS
6.1 DEFINITION
A set is a collection of objects, numbers, ideas etc. The different
objects in the set are called the elements or members of the set.
A set may be defined by using
any one of the following methods:
(i) By listing all the members, for instance, ![]() and
and ![]() . The order does not matter and the elements are listed once
only.
. The order does not matter and the elements are listed once
only.
(ii)
By
listing only enough elements to indicate the pattern and showing that the
pattern continues by using dots ‘![]() ’. For instance,
’. For instance, ![]() .
.
(iii)
By a
description such as ![]() .
.
(iv)
By
issuing an algebraic expression such as ![]() , which means “the set E contains the set of elements,
x, such that x is an integer whose value lies between 2 and 7
inclusive”. (See Set-builder
Notation below)
, which means “the set E contains the set of elements,
x, such that x is an integer whose value lies between 2 and 7
inclusive”. (See Set-builder
Notation below)
6.1.1 ELEMENTS
The elements of a set are the
individual members of that set. For instance, if ![]() , the elements of A are the numbers
, the elements of A are the numbers ![]() and 11. So, since the
number 2 is an element (or member) of A, we can write
and 11. So, since the
number 2 is an element (or member) of A, we can write ![]() , where ‘
, where ‘![]() ’ denotes ‘belongs to’, ‘is a member of’ or ‘is an
element of’.
’ denotes ‘belongs to’, ‘is a member of’ or ‘is an
element of’.
On
the other hand, the number 13 does not belong to the set A and so we can
write ![]() .
.
6.1.2 SET-BUILDER
NOTATION
Commonly used notation for sets on the real line:
![]() is the set of real
numbers
is the set of real
numbers
![]() is the set of positive
real numbers, i.e.
is the set of positive
real numbers, i.e. ![]()
![]() is the set of natural
numbers,
is the set of natural
numbers, ![]()
![]() is the set of
integers,
is the set of
integers, ![]()
![]() is the set of positive
integers,
is the set of positive
integers, ![]()
Example:
(a) ![]() can be written as
can be written as ![]()
(b) ![]() can be written as
can be written as ![]()
(c) ![]() can be written as
can be written as ![]()
(d) ![]() can be written as
can be written as ![]()
(e) The
set of positive real numbers less than 3 can be written as ![]()
In the above, ‘n’, ‘p’ and ‘x’
are dummy variables.
6.1.3 ORDER OF A
SET
The order of a set is the number of
elements contained in the set. For example, if ![]() , then we write
, then we write ![]() .
.
6.1.4 TYPES OF
SETS
(i) FINITE
SETS
These
are sets in which all the elements can be listed, such as ![]() .
.
(ii) INFINITE
SETS
These are sets in which it is
impossible to list all the elements. For instance, ![]() .
.
(iii) EMPTY OR NULL SET
A set with no elements is known as
an empty set (or null set), denoted by ![]() or
or ![]() .
.
Example: ![]()
(iv) EQUAL SETS
Two sets A and B are
equal if they have the same elements. This is written as ![]() . For instance,
. For instance, ![]() .
.
(v) SUBSETS
If all members of a set A
are also members of the set B, then A is said to be a subset of B.
For instance, consider the sets ![]() Then,
Then,
A is a subset of C,
written as ![]() .
.
Also, ![]() .
.
However, we note that ![]() . A is called a proper subset of C, denoted
by
. A is called a proper subset of C, denoted
by ![]() .
.
Hence, If ![]() , then
, then ![]()
If ![]() , then
, then ![]()
Also, for any set A,
![]()
(vi) UNIVERSAL SET
The universal set for any
particular problem is the set which contains all the available elements for the
problem. Thus if the universal set is all the odd numbers up to and including
11, we write ![]() .
.
(vii) COMPLEMENT OF A SET
Consider ![]() and
and ![]() . We define the set
. We define the set ![]() which consists of all
the elements not in P, so
which consists of all
the elements not in P, so ![]() and is called the complement
of P.
and is called the complement
of P.
Hence, if ![]() is the universal set,
the complement of P is the set
is the universal set,
the complement of P is the set ![]() .
.
6.2 INTERSECTION
AND UNION OF SETS
6.2.1 VENN
DIAGRAM
The
pictorial representation of the relationship between sets is called a Venn
diagram.
 Example:
Example: ![]() and
and ![]() .
. ![]() can be represented by
the following Venn diagram:
can be represented by
the following Venn diagram:
Example:
Consider ![]() ,
, ![]() and
and ![]()
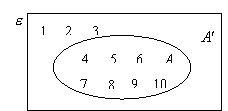
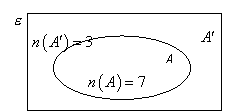
The above Venn diagrams illustrate two different ways of representing the sets. Instead of listing the elements in each set, we can write down the number of elements of each set as shown in the diagram on the right.
Note: If ![]() is a universal set and
A is any set, then
is a universal set and
A is any set, then
![]()
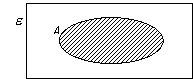
In order to identify a set in a Venn
diagram, we shade the region representing a set A as shown:
6.2.2 INTERSECTION OF
SETS
The
intersection of set A and set B is the set which contains all the
elements that are elements of both set A and set B and is denoted by ![]() .
.
That
is ![]()
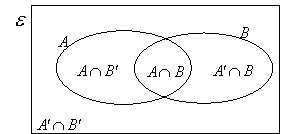
 Two
sets A and B are disjoint
Two
sets A and B are disjoint ![]()
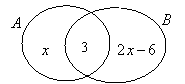 Example: A and B
are two sets and the number of elements in each set is shown in the Venn
diagram. Given that
Example: A and B
are two sets and the number of elements in each set is shown in the Venn
diagram. Given that ![]() , calculate
, calculate
(a) the value of x, (b) ![]() and
and ![]() .
.
Solution: (a) ![]()
![]()
(b) ![]()
![]()
6.2.3 UNION OF
SETS
The union of set A
and set B is the set which contains all the elements that are either
elements of set A or set B or in both, and is denoted by ![]() .
.
That is ![]()
Venn Diagrams:

In general, for any set A and the universal set ![]() ,
,
![]() and
and ![]()
Example 1: Let ![]()
![]()
![]()
![]()
![]()
Describe
the members of the following sets:
(a) ![]() (b)
(b) ![]() (c)
(c) ![]() (d)
(d) ![]()
Solutions:
Example 2: Given that ![]() is the universal set
and
is the universal set
and ![]() , in separate Venn diagrams, shade the sets:
, in separate Venn diagrams, shade the sets:



(a) ![]() (b)
(b) ![]() (c)
(c) ![]()


(d) ![]() (e)
(e) ![]() (f)
(f) ![]()


(g) ![]() (h)
(h) ![]() (i)
(i) ![]()
Example 3: In the Venn
diagrams below, shade the sets:
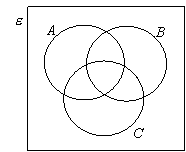
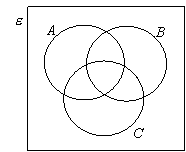
![]()
![]()
Example 4: ![]() ,
, ![]() and
and ![]() . Find
. Find ![]() and
and ![]() .
.
6.3 SET OF REAL
NUMBERS ON THE REAL LINE
The
set ![]() and
and ![]() can be represented
graphically on the REAL LINE as shown below. With the aid of the graphical
representation, the sets
can be represented
graphically on the REAL LINE as shown below. With the aid of the graphical
representation, the sets ![]() and
and ![]() can be obtained as
shown below:
can be obtained as
shown below:
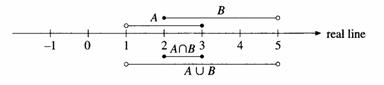
From the above,
it is clear that ![]() and
and ![]() .
.
6.4 SET OF POINTS
IN A PLANE
 The set L denotes the set of points on the
line
The set L denotes the set of points on the
line ![]() in the Cartesian
plane. So,
in the Cartesian
plane. So, ![]() . For example, since
. For example, since ![]() is a point on the
line,
is a point on the
line, ![]() . Since
. Since ![]() is not a point on the
line,
is not a point on the
line, ![]() .
.
6.5 APPLICATIONS
Example: (a) G and H are sets of students
who study Geography and History respectively. Using the letters G, H,
set notation and ![]() to represent set
members, write down an expression for the following statements:
to represent set
members, write down an expression for the following statements:
(i)
“x is a member of the set of students who
study both Geography and History”,
(ii)
“x is a member of the set of students who
study only History”.
Illustrate,
by shading on a Venn diagram, the region that ![]() could lie in.
could lie in.
(b) There are 32 students in a class
and each studies at least one of the subjects: Geography or History. Of these,
22 study Geography and 15 study History. By drawing a Venn diagram, find the
number of students who study both History and Geography.
Solution: (a)
(i) ![]() and
and ![]() . Hence
. Hence ![]() .
.
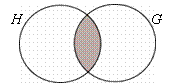
 (ii)
(ii) ![]() and
and ![]() . Hence
. Hence ![]() .
.
(b) Let ![]()
and ![]()
Then
![]()
Let ![]()
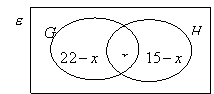
Then
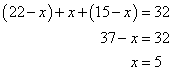
Hence
there are 5 students who study both Histoy and Geography.
Practice
1. In a group of 20
students, 14 play badminton, 9 play table tennis and ![]() do not play either of
the games.
do not play either of
the games.
(a)
If ![]() , find the number of students who play both games.
, find the number of students who play both games.
(b)
If ![]() , find the greatest possible value of
, find the greatest possible value of ![]() .
.
Solution:
(a)
Let ![]() ,
,
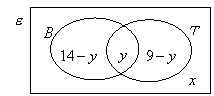
![]() ,
,
and
![]() .
.
If
![]() , we have
, we have
![]()
Thus
the number of students who play both games is 3.
 (b)
(b) ![]() has the greatest value when
has the greatest value when ![]() is the smallest.
is the smallest.
Hence
![]()
Thus
the greatest value of x is 6.
2. A
group of students was given a choice to study the subjects – physics, chemistry
and biology. The Venn diagram shows some of the information about their
choices.
 (a) Given that 30
students took physics and 25 students took chemistry, find
(a) Given that 30
students took physics and 25 students took chemistry, find
(i) the
value of ![]() ,
,
(ii) the
number who took physics only,
(iii) the
number who took at least two of the subjects.
(b) Given
also that 50 students were in the group, and each of them took at least one of
the subjects, calculate the number who took biology only.
[Ans:
6, 14, 22, 9]
3. Of the 24 students in a class, 18 like to play basketball
and 12 like to play volleyball. It is given that
![]()
![]() and
and
![]() .
.
Let ![]() and draw a Venn
diagram to illustrate this information.
and draw a Venn
diagram to illustrate this information.
(a)
Describe the set ![]() and express
and express ![]() in terms of
in terms of ![]() .
.
(b)
Find the smallest possible value of
![]() .
.
(c)
Find the largest possible value of ![]() .
.
[Ans:
![]() , 6, 12]
, 6, 12]