Investigation Worksheet 1 on Venn Diagrams

Consider the following Venn diagrams:

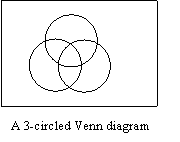
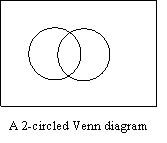
Notice that the 2-circled Venn diagram is divided into 4 separate regions while the 3-circled Venn diagram is divided into 8 separate regions. There are only 2 separate regions in a 1-circled Venn diagram.

Question: What is the maximum number of separate regions you can get for an n-circled Venn diagram? (n is any positive integer)

In order to answer the question, you may want to first try the following:

1. Make a guess and verify your guess with a 5-circled or a 4-circled Venn diagram.

2. Study the two 4-circled Venn diagrams below:

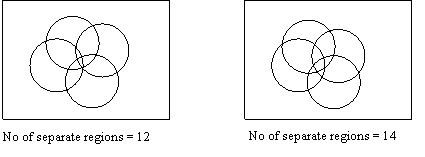
Investigate with other 4-circled Venn diagrams.

What is the maximum number of separate regions in a 4-circled Venn diagram? How do you know it is the maximum?

3. Devise a method of drawing n-circles in a Venn diagram so that the number of separate regions is a maximum.

4. What is the maximum number of intersection points in an n-circled Venn diagram?

5. Investigate a way in which you can link the number of separate regions to the number of intersection points.

Now answer the question set in the beginning.